-2o1o- Cryptanalysis of Caesar Cipher

In cryptography, a Caesar cipher, also known as a Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a shift of 3, A would be replaced by D, B would become E, and so on. The method is named after Julius Caesar, who used it to communicate with his generals.

[Quoted from Wikipedia.org]

I found this cipher suit simple yet interesting, hence I brainstormed to program an utility out to perform the encryption process. You can download it here.

To encrypt a plaintext, you have to first call the insertPlaintext() method, and insert the required arguments. This method accepts only two arguments: the plaintext and the number of shifts. For instance, suppose ce is the instance of Caesar_CA() that I've created, in order to encrypt the string "testing" with the rows shift of 8, I will have to type this:

ce.insertPlaintext("testing",8);

Followed by an explicit method call of encrypt(),

ce.encrypt();

However the encrypt method does not invoke the method to display the encrypted text, you have to call the System.out.println() or similar method to display the string returned by the displayCiphertext() method. For instance,

System.out.println(ce.displayCiphertext());

Finally, the output would be

|m{|qvo

Now it comes to the interesting part; we are going to discuss about the way to decipher the ciphertext without the knowledge of the number of rows shifted through cryptanalysis. I do realise that the term cryptanalysis may be completely new to some of you, but don't worry as it doesn't require a genius to understand the underlying concept of it. Conversely, once you've gotten the hang of it, you will begin to find it interesting. In short, Cryptanalysis is the study of translating the ciphertext back into the plaintext.

For the purpose of guiding you from the scratch, I shall use the cipher suit that you are already familiar with. Take the aforementioned case as example, shifting row of the plaintext "testing" by 8 would produce the ciphertext "|m{|qvo". The decrypting process is comparatively simple, all it does is only basically reshifting the rows of the text back to its previous state. This also applies to most of the asymmetric encryptions; if you have the private key, you can decrypt the ciphertext at any point of time. Now it comes to the tricky part, also the gist of what I'm trying to deliver to you. What would happen if you do not have the private key?(in Caesar, private key is similar to the number of shifted rows) Will you still be able to obtain the initial form of the ciphertext?

The answer is obviously yes, virtually every encryption algorithm has its own way to retrieve the plaintext-form of the ciphertext's. Don't get me wrong, theoretically retrieveable does not imply that it's retrieveable in practice. Take the hash I've gotten from challenge spoofing for example: the Windows XP NTLM Security Session hash. In theory its perfectly possible to obtain the plaintext, that is, by performing an exhaustive search brute force attack. However the whole process of brute forcing would take more than millions or even billions of years, and just so you know there's no one that is silly enough to spend his/her entire life just for breaking a hash nor does he/she can live for that long. Consequently, it's practically impossible for a person to break a strong encryption but for a simple and weak encryption algorithim like Caesar, it's both theoretically and practically breakable.

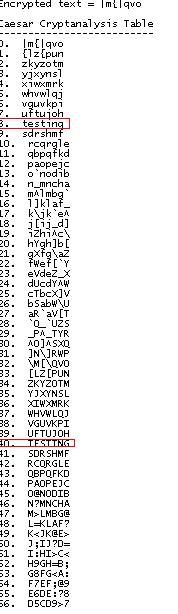
In Caesar, since there are only a limited number of possible shifts.(26 for alpha combinations) One way to achieve the goal is to list out all the possible shifts in a tabular form. The program you downloaded above will demonstrate how it is done.

First, you have to call the method insertCiphertext() and pass the ciphertext into the argument. After which, you call the System.out.println() method to print the table returned by the cryptA() method.

Lastly,