-2o1o- Web Spambot v1.1.5 released!

After a few days of consideration again I've decided to release this program again, lol how indecisive I am.

Warning : Please be informed that excessive usage of this program could lead to a malady known as Denial of Service(DoS)/Distributed Denial of Service(DDoS) attack that may land you in court, and that could result in a sentence of up to a few years of imprisonment should you be found guilty. Use this program only for testing purposes or with the consent of others parties. Personally as a white hat hacker I myself do not advocate that nor am I responsible for any form of damage or harm incurred from the misuse of this program.

Overview of the program

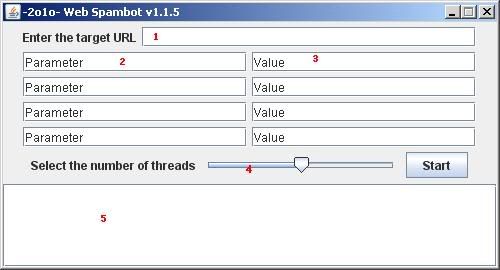
1. The target URL

2. The parameter of the POST request

3. The value of the parameter

4. Number of threads to be used

5. The status message box

In order to further increase your understanding to operate this program, I’ll perform a live demo on one of the web hosted on my webserver. Take a look at the number of registered account, 3175; which means currently there’s an amount of 3175 accounts in my database.

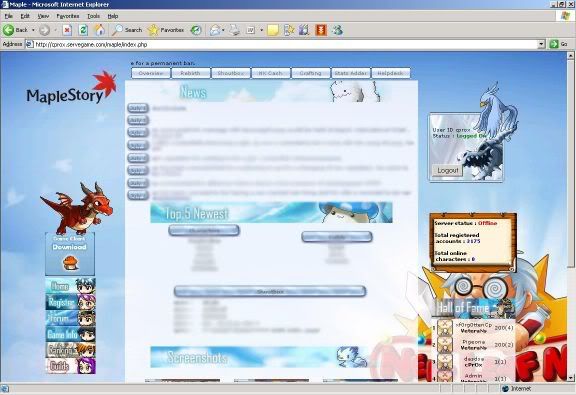
The screenshot below shows the registration form of the site. There are four mandatory fields to be filled, therefore the web spambot has to load four parameter/value fields, notwithstanding the availability of hidden fields. However this isn’t what we are going to deal with; unless you are unsure of the what value to be filled into a particular field and would like to discover the pattern of the acceptable values by playing around with the form. The main purpose of us visiting this page is to view the source code and extract the required information to perform the attack.

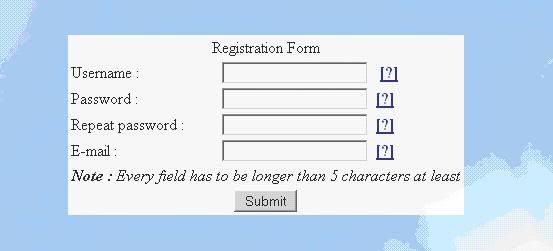
For your viewing convenience, I’ve copy pasted the source code of the registration page and marked the important elements that you should take note of. The value in red box is the page that handles the registration form’s POST requests, and it should only have one in every form. The values in blue box on the other hand are the parameters of the form, the number of parameter in a form does not have a fixed value, and the number may vary time to time. In this case we have a total of four parameters: the reg_id, the reg_pw, the reg_pw2, and the reg_email. Now we’ve gathered enough information to launch an attack.

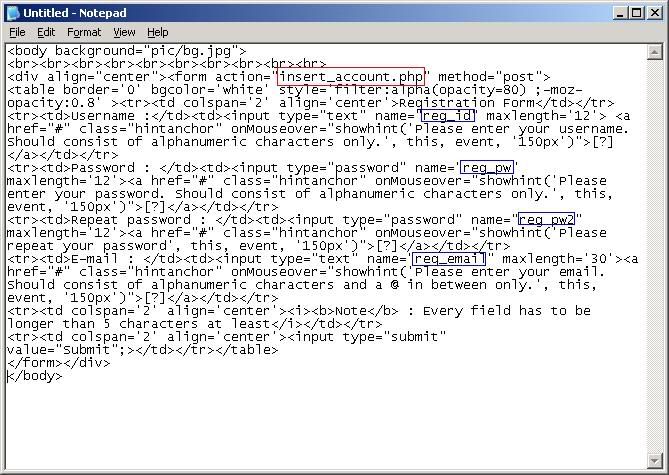
Since there are four parameters in the form and assume that I want to flood the web with 300 accounts, I would have –n 300 -p 4 as the arguments to be passed to the program.

-n denotes the number of POST requests

-p denotes the number of parameters

This is how the fields should look like:

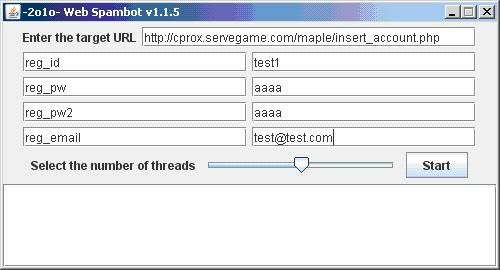
click Start

and

.......

Done! 299 successive POST requests sent(299 registered accounts) in 17843 milisecs(17.8 secs).

That’s amazingly so much of deviation from the previous version of web spambot(around 74% of performance boost, not taking into account the connection latency and the nature of network performance being fluctuant when handling excessively lots of packets)

A screenshot of the database

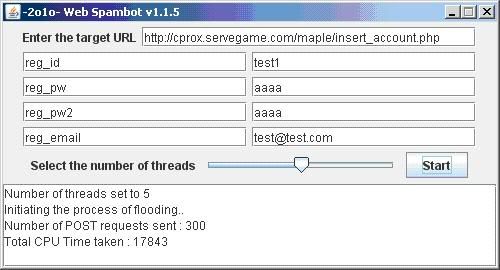
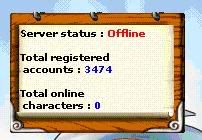
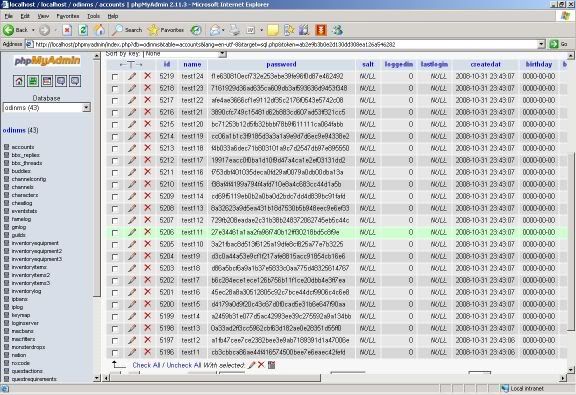
Pretty neat eh?


Warning : Even if you have the wrong parameters filled, by clicking start you and the target host would still consume considerably amount of bandwidth; the same thing happens even if the target host has your IP blocked/blacklisted, because technically the process of examining the source IP and discarding packets consumes bandwidth as well.

Number of threads versus Performance

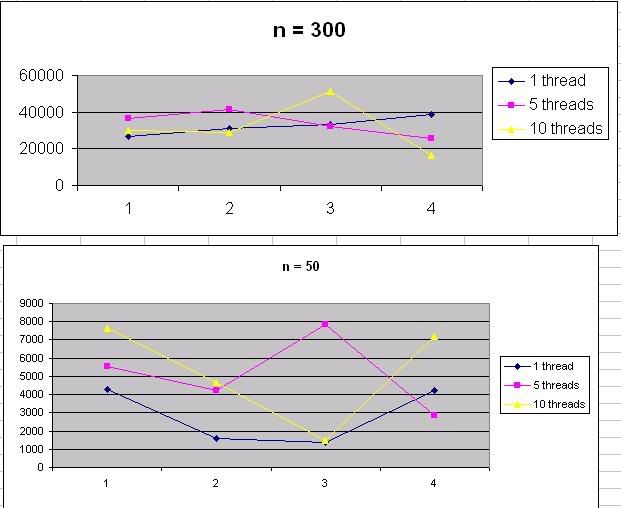
I've done a study to find out the relation between the number of threads and performance in this program using Microsoft Excel with number of POST requests, n being 50 and 300. The result of the findings turned to be somewhat out of my expectation and I don't see a clear relation of the number of threads versus performance in this program as illustrated above. For now just stick to whatever number of threads you like, I will be revising the program again after I've done with my school exams and assignments.


Addons
The class diagram


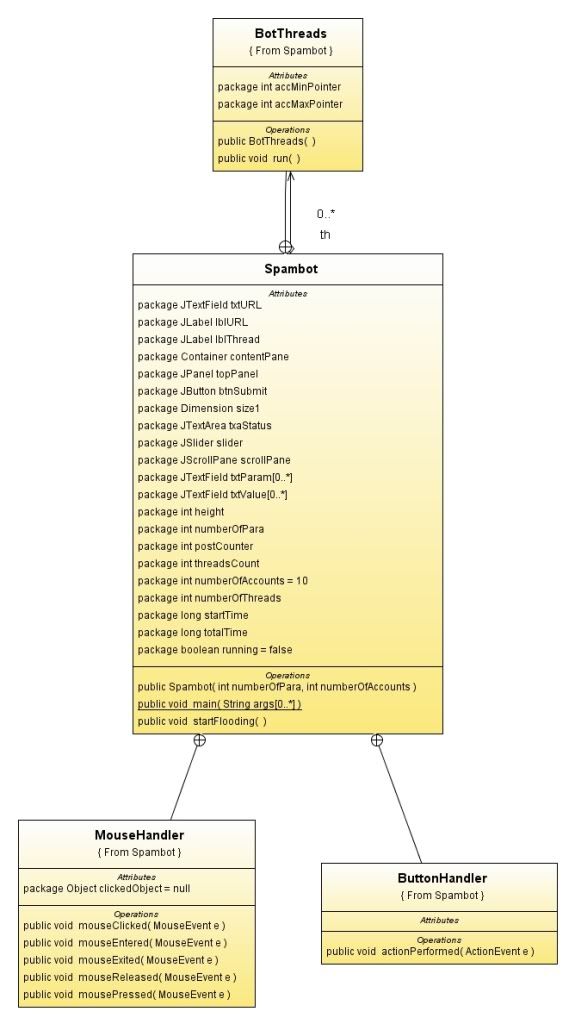
Download link : Javadocs + Source code + JAR executable + Class diagram in a bundle

Web spambot

Managed to get the spambot prototype done two days ago; I've used it on my web server and to my surprise the spambot was able to register up to 300 accounts in approximately 30 secs(that's around 860k accounts per day operating on a single-threaded environment). 

Gonna add some enhancements like performance enhancement, GUI and multi-threading support after I got my assignments done.

Note : I realized that if this program were to be used for non-legitimate purposes the damage that  it would inflict could be significant, hence I won't be releasing this program to the public.

-2o1o- Cryptanalysis of Caesar Cipher

In cryptography, a Caesar cipher, also known as a Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a shift of 3, A would be replaced by D, B would become E, and so on. The method is named after Julius Caesar, who used it to communicate with his generals.

[Quoted from Wikipedia.org]

I found this cipher suit simple yet interesting, hence I brainstormed to program an utility out to perform the encryption process. You can download it here.

To encrypt a plaintext, you have to first call the insertPlaintext() method, and insert the required arguments. This method accepts only two arguments: the plaintext and the number of shifts. For instance, suppose ce is the instance of Caesar_CA() that I've created, in order to encrypt the string "testing" with the rows shift of 8, I will have to type this:

ce.insertPlaintext("testing",8);

Followed by an explicit method call of encrypt(),

ce.encrypt();

However the encrypt method does not invoke the method to display the encrypted text, you have to call the System.out.println() or similar method to display the string returned by the displayCiphertext() method. For instance,

System.out.println(ce.displayCiphertext());

Finally, the output would be

|m{|qvo

Now it comes to the interesting part; we are going to discuss about the way to decipher the ciphertext without the knowledge of the number of rows shifted through cryptanalysis. I do realise that the term cryptanalysis may be completely new to some of you, but don't worry as it doesn't require a genius to understand the underlying concept of it. Conversely, once you've gotten the hang of it, you will begin to find it interesting. In short, Cryptanalysis is the study of translating the ciphertext back into the plaintext.

For the purpose of guiding you from the scratch, I shall use the cipher suit that you are already familiar with. Take the aforementioned case as example, shifting row of the plaintext "testing" by 8 would produce the ciphertext "|m{|qvo". The decrypting process is comparatively simple, all it does is only basically reshifting the rows of the text back to its previous state. This also applies to most of the asymmetric encryptions; if you have the private key, you can decrypt the ciphertext at any point of time. Now it comes to the tricky part, also the gist of what I'm trying to deliver to you. What would happen if you do not have the private key?(in Caesar, private key is similar to the number of shifted rows) Will you still be able to obtain the initial form of the ciphertext?

The answer is obviously yes, virtually every encryption algorithm has its own way to retrieve the plaintext-form of the ciphertext's. Don't get me wrong, theoretically retrieveable does not imply that it's retrieveable in practice. Take the hash I've gotten from challenge spoofing for example: the Windows XP NTLM Security Session hash. In theory its perfectly possible to obtain the plaintext, that is, by performing an exhaustive search brute force attack. However the whole process of brute forcing would take more than millions or even billions of years, and just so you know there's no one that is silly enough to spend his/her entire life just for breaking a hash nor does he/she can live for that long. Consequently, it's practically impossible for a person to break a strong encryption but for a simple and weak encryption algorithim like Caesar, it's both theoretically and practically breakable.

In Caesar, since there are only a limited number of possible shifts.(26 for alpha combinations) One way to achieve the goal is to list out all the possible shifts in a tabular form. The program you downloaded above will demonstrate how it is done.

First, you have to call the method insertCiphertext() and pass the ciphertext into the argument. After which, you call the System.out.println() method to print the table returned by the cryptA() method.

Lastly,

-2o1o- Does MTU affect your network latency?

As most of you might have already aware about, there are a few common factors that bear potential to affect the overall network performance, such as the size of bandwidth, the distance between two sending and receiving nodes, the quality of the transmission medium, the strength of the wireless signal etc. Now I'm going to discuss about something other than the common factors that affects the overall network performance, the MTU.

For simplicity's sake, I shall not confuse you passages of purple prose regarding MTU. The short yet understandable definition of MTU: MTU(Max Transmission Unit) is the maximum size of packet being sent across network without being fragmented. The pertinent question being posed is that, "How does MTU affects the latency of a network?".

I do aware that the you as the one reading this might be a computer geek that does lots of network related stuff daily and you might think that since MTU is only a measure of the maximum size of a packet before it gets fragmented, the increment/decrement of its size would only affect the number of packets being fragmented across network and it would not affect the total capacity of a network, let alone the transmission speed. However, the nature of the network is that, every packet fragments will have a network frame attached to it. What a frame does that it carries the information like source/destination address, frame sequence, checksum, TTL, so that the intended recipient knows that the packet belongs to it upon reception by looking at the destination address. The recipient then assembles the fragmented packets in accordance with the frame sequence. 

Consequently, it's necessary for every fragmented packets to have a frame attached so that it can be received by the intended recipient and be assembled into its initial form. In conclusion, the smaller the MTU size is, the more fragments a packet need to break into, the more frames need to be sent and ultimately it leads to heavier network overhead.

-2o1o- An Example of RSA Algorithm

An example of RSA encryption algorithim quoted from www.wikipedia.org

(Click to enlarge)

RSA is an asymmetric encryption algorithm that features public key cryptography technology. I've written an example of RSA encryption in Java, you can download it here. Dont fret if you dont understand it at the first glance; It's not as hard as how it seems, I will go through part by part of the program with you.

import java.math.BigInteger;

Since the primitive data types in Java does not support huge integers that is essentially required in RSA, I've imported the BigInteger class as an approach for such deficiency. For more information about BigInteger. Click here. 

System.out.println("Generating Public and Private keys..");

n = p * q;

z = (p-1) * (q-1);

Note : In this case we assume the totient p(n) as z

RSA requires a pair of key called the public key and the private key pair. Public key is meant to be distributed over the world for encrypting purpose whereas private key is meant to be kept in personal for decrypting purpose. In order to achieve this, first we will have to define two prime numbers. I will use 11 and 13 for simplicity's sake, but bear in mind that in a real situation the primes are very likely to be over more than 100 digits, and the computation of the whole process usually takes lots of CPU resources and time, hence RSA is far slower than DES and other symmetric cryptosystem. The code n = p * q; describes the process of n = pq. On the other hand, z = (p-1) * (q-1) describes the process of computing (p-1)*(q-1). The processes above compute the values n and z and this completes the public key pair. 

for (int i=3;i<=z;i++) {

if ((z % i)!=0) e=i;

for (int x=0;x<=z*3;x++) { //x has to be at least 1 time larger than z which carries the value of (p-1) * (q-1)

if (((e*x) % z) == 1) {

d = x;

}

}

}

The code above shows the process of generating one of the private key entry e, which has to be relatively prime to the value z. It also shows the generation of the private key exponential where de = n mod 1. These two values has to be kept secret.

public BigInteger encrypt(int enc) {

enc2 = BigInteger.valueOf(enc);

n2 = BigInteger.valueOf(n);

encPowE=enc2.pow(e);

encPowEModN = encPowE.mod(n2);

return  encPowEModN; //returns the encrypted message

}

The program first assigns the value of enc into the BigInteger instance enc since the method pow() can only be invoked by an instance of BigInteger. Likewise, n2 carries the value of n for the purpose of invocation for the method mod(). The process above can be shown with the equation as follows

where 

enc = the message to be encrypted

e = the relative prime of the computation of (p-1) * (q-1), z

n = computation of pq

Encrypt(enc) = (enc^e) MOD n

Assume 52 is the value we are going to encrypt, so the equation would be

Encrypt(52) = (25^119) MOD 143

           

equivalent to 103. 

public BigInteger decrypt(int decr) {

decr2 = BigInteger.valueOf(decr);

decrPowD = decr2.pow(d);

decrPowDModN = decrPowD.mod(n2);

return  decrPowDModN ; //returns the decrypted message

}

Now it comes to the decrypting part, similar to the encrypting part, the decr2 instance holds the value of decr, also the ciphertext. The process is shown as follows

where 

decr = the ciphertext to be decrypted

d = the private key exponential

n = the computation of pq

Decrypt(decr) = (decr^d) MOD n

so it would be,

Decrypt(103) = (103^359) MOD 143

and Voila! You got the decrypted message 52!

2o1o- Basic Mobile Application Programming Guide

First you have to download and install all the required programs listed as follows:

• Microsoft ActiveSync
• Microsoft Visual Studio 05/08
• Windows Mobile 6 SDK

The setups for the files are pretty much straightforward so I guess it won’t be of much problem for you to get the installations done.

When everything is done, launch the Microsoft Visual Studio and select File -> New Project, expand Visual Basic and click Smart Device Project and then select Smart Device Project at the right portion of the windows. You may change the name if you wish to; press OK when everything is done.

Next, a dialog similar to the picture below should appear, make sure that you’ve selected the right Target platform and .Net Framework version.(It’s not a necessity to have the same settings as what shown in the picture). Press OK when you’re done.

Design your form similar to the layout shown in the picture below. Again, it’s not a necessity to follow everything exactly. Just make sure that you have two textboxes for the username/password, a login button, and codes that validates the username/password combination.

Similarly, design your form in accordance with the layout shown in the picture below. The recipient groups’ checkboxes allow you to specify your target recipient. Note that within the simulative environment recipient’s number can be any combination of numbers such as 02528335 or even 1234567. For instance, suppose you have the Marketing Dept and Finance Dept checkboxes ticked, the two departments have the number of 00000 and 00001 defined respectively. Upon the transmission of the SMS, the mobile phones having the number 00000 and 00001 will receive the SMS.

The piece of code that does the SMS sending to the emulator is as follows:

where 

h = The number of the recipient. For example you can do retrieve the number from a textbox like txtRecipient.text

g = The message to be sent. For example txtMessage.text

Dim VBMobileSMS As New SmsMessage(h, g)

VBMobileSMS.Send()

Before that, you have to import an external library first(place this at the topmost of the program)

Imports Microsoft.WindowsMobile.PocketOutlook

Note : If you encounter an error stating that the library could not be found, go Projects -> Add Reference and select Microsoft.WindowsMobile.PocketOutlook under .NET

Once you’ve gotten the design/coding done, hit F5 once or click the green arrow-like button, a windows should appear, asking you to select an emulator to deploy for the program. Personally I prefer running my mobile programs using Windows Mobile 6 Professional Emulator, but of course ultimately the choice is still yours. (As far as I know the difference in the type of emulator chosen does not affect your programs in any way, except the appearance of course.) Most importantly, make sure that your cell emulator is running else the emulator would not load.

Next, a mobile emulator should appear and your program will be loaded into the emulator as well. Now try to send a simple SMS, you should be able to see the message you typed in the cell emulator, similar to the picture below.

If you encounter an error stating that the COM port is unavailable or similar, check the bottom left of your cell emulator program, you should be able to see which port your cell emulator is currently using. Now go back to the deployment of the mobile emulator select File -> Configure -> Peripherals, under Serial Port 0, type in the port that you’ve gotten from the cell emulator.

You can download the program here.

CABAL : High attack or high crit damage/rate?

Some calculations i made to calculate the efficiency of
Red Osm single slotted weapon vs deathblow titan double slotted

Character build
rol+1 x 2 20% crit rate
lightning blade 15% crit rate
ice blade 10% crit rate
character base 5% crit rate
50% total crit rate

helm 20% crit dmg
titan(slot extended) 48% crit dmg / red osm 20% crit dmg
ice + lightning 20% crit dmg
character base 20% crit dmg
108% total crit dmg / 80% total crit dmg

eof+8 5% amp
bof+3 x2 10% amp
boots/suit/glove 21% amp
36% total amp


total atk with titan/phery 700
total atk with redosm/topaz 770

cr = crit rate
cd = crit dmg
sw.amp = sword amp
ch.amp = character amp
sk.amp = skill amp
sk.atk = skill atk
ch.atk = character atk


Formula to calc output damage
Damage rating = (cr/100)*((((sk.amp+(ch.amp/100))*ch.atk)+sk.atk)+((((sk.amp+(ch.amp/100))*ch.atk)+sk.atk)*(cd/100)))


titan phery estimated output damage= no amp involved* = (50/100)*(((1.7*700))+904)+((1.7*700)+904)*(108/100))) = 0.5*(2094+(2094*1.08)) = 2177.76

redosm topaz estimated output damage= (50/100)*(((1.7*770))+904)+((1.7*770)+904)*(80/100)))no amp involved* = 0.5*(2213+(2213*0.8)) = 1991.7

titan phery estimated output damage with 36% amp= (50/100)*(((2.06*700))+904)+((2.06*700)+904)*(108/100)))= 0.5*(2346+(2346*1.08))= 2439.84

redosm topaz estimated output damage with 36% amp= (50/100)*(((2.06*770))+904)+((2.06*770)+904)*(80/100)))= 0.5*(2490+(2490*0.8))= 2241.00

therefore we can deduce that db titan > red osm(higher damage rating)

Solution for "Cannot find eksplorasi.exe"

1. Start -> Run -> Regedit
2. HKEY_LOCAL_MACHINE>SOFTWARE>Microsoft>Windows NT>CurrentVersion>Winlogon(Note : always consider making a backup of your regedit settings everytime before submitting any changes should any problems occur later on)
3. In the right panel of the regedit windows, you should be able to see Shell = "Explorer.exe "%Windows%\Eksplorasi.exe""
4. Delete "%Windows%\Eksplorasi.exe" located beside explorer.exe and you're done
Example : shell="Explorer.exe"