-2o1o- Birthday Attack!

The Birthday Paradox

In probability theory, the birthday problem, or birthday paradox[1]
pertains to the probability that in a set of randomly chosen people some pair of
them will have the same birthday. In a group of 23 (or more) randomly chosen
people, there is more than 50% probability that some pair of them will both have
been born on the same day. For 57 or more people, the probability is more than
99%, reaching 100% as the number of people reaches 366.[2] The mathematics
behind this problem leads to a well-known cryptographic attack called the
birthday attack. [Wikipedia.org]

“How many birthdays does a person have in a year?”
“One”
“Then assume in a group of 23, how do we calculate the probability of a person having the same birth date as another?”
“Since the probability of one person’s birthday falls on a day is 1/365, so in a group of 23 it would be 23/365 = 6.3%”
(not taking the presence of leap years into account)

WRONG

So what’s the right way of answering this?
The simpler version of formula is
(number of people * (number of people – 1) ) / 2
(23 * 22) / 2 = 253 pairs

If you’re so inclined to find out the proper way of solving the case above, you can search for permutations and combinations on the web. Yea, and be prepared to work with big numbers.

Next, we calculate the probability of one person’s birthday DOESN’T fall on a day, and that would be
364/365 = 0.99726 (99.72%) it seems really big now but trust me, after a number of self multiplication, it shrinks really fast

we then apply the 253 as the exponent since now we are trying to get the probability of 253 pairs(group of 23).

and it would be

0.99726^253 = 0.4995 (49.95%) get what i was trying to say?

Now we’ve gotten the probability, but we are not done yet. Note that we were only focusing on the problem scenario (with the keyword DOESN’T), so in order to get the probability of a group of 23 sharing the same birth date we would do

1 – 0.4995 = 0.5005 (50.05%)

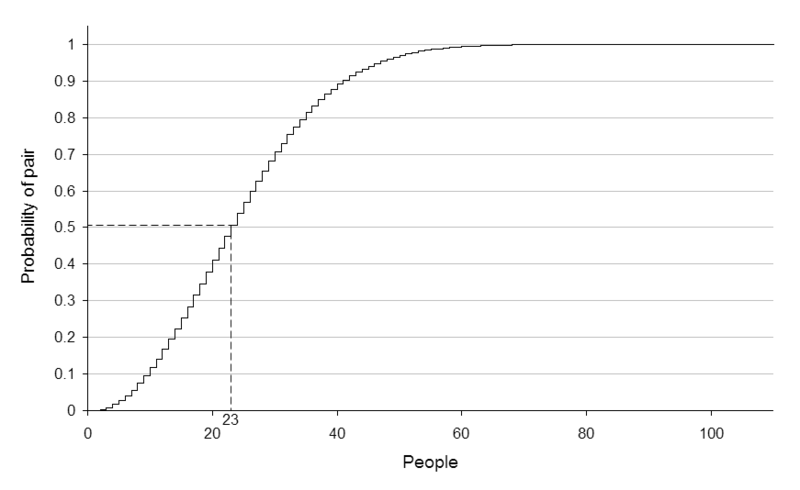
A graph showing the approximate probability of at least two people sharing a birthday amongst a certain number of people.


Now that we’ve calculated the number of pairs, the problem scenario’s probability and the actual probability. So what does it got to do with cryptography?

The Digital Signature
We are proceeding to the interesting part; let’s take the common archetypes in cryptography as an example: Alice, Bob, Mallory, Carol and Bob. Suppose that Alice wants to send an encrypted letter to Carol, and with the content that she wants to recommend Dave as the IT manager in the company, her letter would look something like

Dear Carol,
I would like to recommend Dave as the IT manager of our company because from my observation he has the potential to handle the role as an IT manager. Furthermore he is hardworking and does not late..

Then the Alice would digitally sign the letter using PGP(Pretty Good Privacy) and hand it to her secretary Mallory. However due to some personal disputes Mallory had with Dave, Mallory does not want Dave to hold the position. Hence, she would write another letter to stop Dave from getting the job and the letter would look like

Dear Carol,
I feel that Dave is not a perfect candidate for the role as the IT manager because he is often late and does not show any commitment in his work. Furthermore he does not know how to cooperate with his colleagues..

Indeed this letter would be perfect for Mallory to achieve her goal, but obviously Carol would not sign this letter and it is computationally infeasible for Mallory to obtain the private key from the digital signature. To further enhance your understanding on how the Birthday Attack takes place in this scenario, I will break down the following explanation into steps.

1. Alice is given two keys. One is called the public key and another one is called the private key.
2. The public key is given to anyone who needs it, but the private key is kept to her only.
3. Both one of the key can encrypt the data and the other key can be used to decrypt the data
4. Alice can encrypt the letter using her private key and Carol can decrypt the letter thereafter using her public key and vice versa. Mallory has the access of the encrypted letter but without the Alice's private key she can do nothing with it.
5. In order to sign a document, Alice will convert the letter into just a few lines by a process called “hashing” (ie: MD5, SHA). These few lines are called the message digest, and since it was created using one-way-hash function, it cannot be reverted back to its initial plaintext form.
6. Alice then encrypts the message digest using her private key and that would produce the digital signature.
7. Alice attaches the digital signature to the letter and passes it to her secretary Mallory, asking her to pass the encrypted letter to Carol.
8. Mallory decrypts the digital signature back to the message digest form.

A diagram showing how a RSA digital signature is applied and then verified. (DSA and NR differ slightly.) [Wikipedia.org]

We assume that the letter
Dear Carol,
I would like to recommend Dave as the IT manager of our company because from my observation he has the potential to handle the role as an IT manager. Furthermore he is hardworking and does not late..

produces the message digest
iOJfioJcioSJSfioJSVkSMflsdfkLNSgWIjfLImnvcLKFnLhfIOShfIEGNLSnbZLSHgfIHFLHGliHklvNSlgfNSLHISLIhfLnfLIjhgPQOgpGiqojOGVIAOJBKdmaKLdnVJW

and the letter
Dear Carol,
I feel that Dave is not a perfect candidate for the role as the IT manager because he is often late and does not show any commitment in his work. Furthermore he does not know how to cooperate with his colleagues..

produces the message digest
SGIOPDOPvmKFmvklNLSDKFLWGOPvjWIPGKBVmWKLVnLKTJWPFjIPtfwnMCnMFWPGUWJbpJKVCM:LKCMQJFaOIBPOKjfSFjKSfjKSLvjKLvKSjvSjdfjsf

If Mallory were to substitute the second letter with the original one and pass it to Carol, she would be able to tell that the letter has been substituted since the message digest produced by the hashing function of the second letter does not match the message digest produced by the decryption of the digital signature.


The Birthday Attack takes place
Mallory writes the letter again
Dear Carol,
I (feel think) that Dave (is not isn’t) a perfect candidate for the role as the IT manager because (he is he’s) (often always) late and (does not doesn’t) show any (commitment responsibility) in his work. (Furthermore Moreover) he (does not doesn’t) know how to (cooperate work) with his colleagues..

The ( aa bb ) denotes the alternative usage of word, which means either aa or bb can be used to produce different variation of letters while keeping the message conveyance of the letter intact. Since there are 9 combinations of alternative words, Mallory is able to generate up to 2^9 amount of similar letters using all the possible alternative pairs. Mallory would then hash all of the generated letters and given enough of combinations she would eventually be able to come up with a letter with exactly the same message digest as the original one.

For example,
Letter (257/512)
Dear Carol,
I think that Dave is not a perfect candidate for the role as the IT manager because he is always late and doesn’t show any responsibility in his work. Moreover he does not know how to work with his colleagues

Message Digest :
SfiPSJifoSJidfOSJDIONGWIOSNVISjfWPJDiMvNWkjdHSDjASHfuSHfoSHfoWSHfjSHDjhfushfOUShfJShfOSdhAODHOAhfOWSFhSJfhSdjHJSdhUShJfhSJfhJSHFj
(does not match with the original one)

Letter (412/512)
Dear Carol,
I feel that Dave isn’t a perfect candidate for the role as the IT manager because he’s often late and doesn’t show any commitment in his work. Moreover he does not know how to work with his colleagues

Message Digest :
iOJfioJcioSJSfioJSVkSMflsdfkLNSgWIjfLImnvcLKFnLhfIOShfIEGNLSnbZLSHgfIHFLHGliHklvNSlgfNSLHISLIhfLnfLIjhgPQOgpGiqojOGVIAOJBKdmaKLdnVJW
(matches the original one)

Consequently, Carol would not be able to notice that the letter has been altered since the letter generates the same message digest as the digital signature.

The Birthday Attack program

I've written a program to prove the mathematics behind the probability theory. In the program there's only one constructor, accepting two parameters.

public BirthdayAttack(int itemRange,int amount) {

I shall stick to the example given above, using the same itemRange(the days) and the amount(the number of people in a group)

public static void main(String[] args) { BirthdayAttack ba = new BirthdayAttack(365,23); ba.generate(); ba.compare(); ba.calculate(); }

The Output

Generated numbers
-----------------
39
155
191
327
352
163
121
282
8
166
210
182
331
310
29
358
352
285
71
92
66
353
28
--End of number generation--

2 352 spotted

The probability :
50.048%

Download Link(Megaupload)